Diskrétní matematika

Výzkumná skupina se zabývá především zkoumáním otevřených problémů v oblasti kombinatoriky, diskrétní matematiky a teorie grafů. Teorie grafů nachází v posledních desetiletích mnoho aplikací v nejrůznějších oblastech lidské činnosti, od navrhování struktury sítí (elektrických, vodovodních, sociálních) přes přidělování mobilních či vysílacích frekvencí až po různé druhy optimalizace (v dopravě, ve vyhledávání atd.). Skupina se věnuje především studiu speciální třídy grafů odvozených od částečně uspořádaných množin, tzv. cover-incomparability graphs, jejich vlastnostem a složitosti jejich rozpoznávání. Další oblastí, která je v současné době v centru našeho zájmu je studium ekvivalencí na grafech definovaných pomocí různých grafových operací, například tzv. Seidel’s switching.

Oblasti výzkumu

Teorie grafů

Teorie grafů je jednou z matematických disciplín, které nachází různá uplatnění v praxi díky tomu, že pomocí grafů lze modelovat širokou škálu problémů z různých oblastí lidské činnosti od navrhování struktury sítí (elektrických, vodovodních, sociálních) přes přidělování mobilních či vysílacích frekvencí až po různé druhy optimalizace (v dopravě, ve vyhledávání atd.) Jednou z konkrétních oblastí teorie grafů, která je v současné době v centru našeho zájmu, je studium ekvivalencí na grafech definovaných pomocí různých grafových operací, například tzv. Seidel’s switching.

Chemická teorie grafů

Tato oblast výzkumu umožňuje matematickými prostředky studovat některé vlastnosti chemických látek s užitím tzv. molekulárních grafů, jimiž můžeme chemické látky
reprezentovat. Pro molekulární grafy se definují tzv. topologické indexy, které matematickým způsobem vyjadřují určitou vlastnost dané látky a pro něž můžeme použít existující výsledky a postupy z matematiky. V posledních desetiletích byl zaveden značný počet těchto topologických indexů závisejících zejména na vzdálenostech vrcholů, na stupních vrcholů, případně na maticích odpovídajících danému molekulárnímu grafu a jejich spektru.

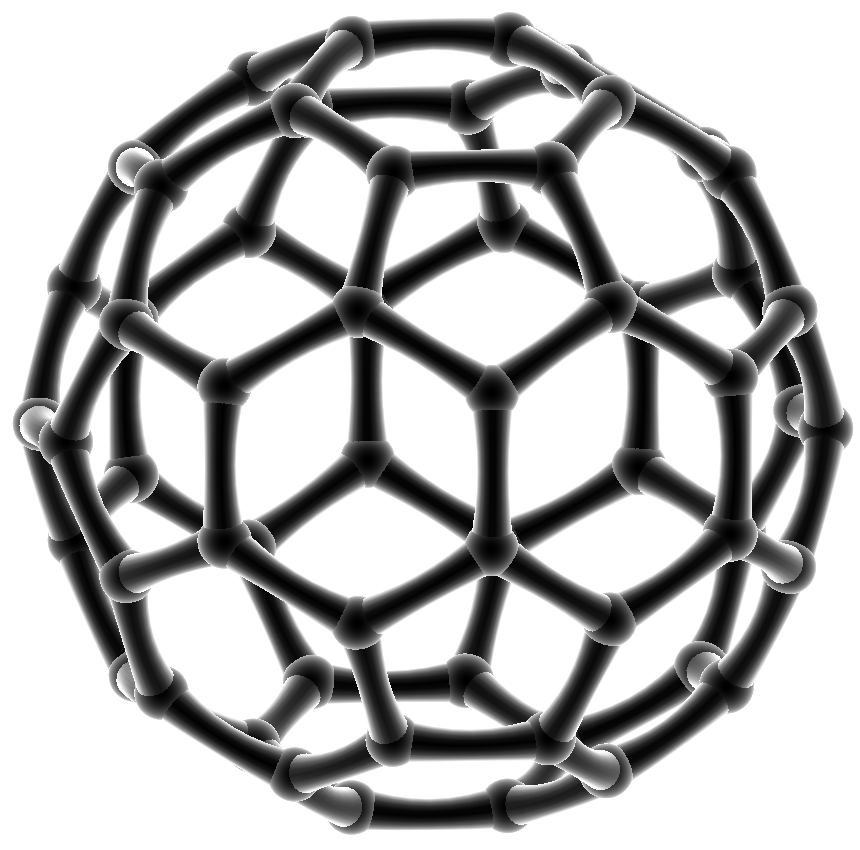
V této oblasti se věnujeme především studiu tzv. Wienerova indexu. Tento deskriptor zavedl v roce 1947 chemik Harry Wiener pro určení aproximačního vzorce bodu varu parafínu. Od té doby se Wienerův index stal jedním z nejčastěji používaných molekulových deskriptorů a v současnosti je využíván především k předběžnému screeningu molekul léčiv. Nás zajímá zejména určování extremálních hodnot Wienerova indexu pro specifické třídy grafů. Specifickou třídou molekulárních grafů, které se také nacházejí v centru naší pozornosti, jsou tzv. fullerenové grafy, tedy molekulární grafy fullerenů, což jsou určité druhy molekul, které jsou v současné době zkoumány jako nové perspektivní materiály například pro techniku nebo lékařství. Fullerenové grafy vyjadřují strukturu těchto molekul a umožňují studovat jejich vlastnosti z matematického hlediska.

Výpočetní složitost

U mnoha otázek je v dnešní době samozřejmostí hledat algoritmy pro efektivní způsoby výpočtu na počítači. Kvalita algoritmů se měří zejména jejich časovou náročností v závislosti na velikosti vstupu. Teorie výpočetní složitosti se věnuje otázkám existence co nejefektivnějších algoritmů, případně také dokazování, že algoritmy s danými vlastnosti neexistují (nebo že je jejich existence z hlediska současného poznání informatiky velice nepravděpodobná). V oblasti teorie grafů a také chemické teorie grafů již existuje řada výsledků v oblasti výpočetní složitosti. Zaměřujeme se na zkoumání těchto algoritmů a jejich případné zrychlení nebo nalezení algoritmů nových.